[10000印刷√] ルート 展開 近似 399250-ルート 展開 近似
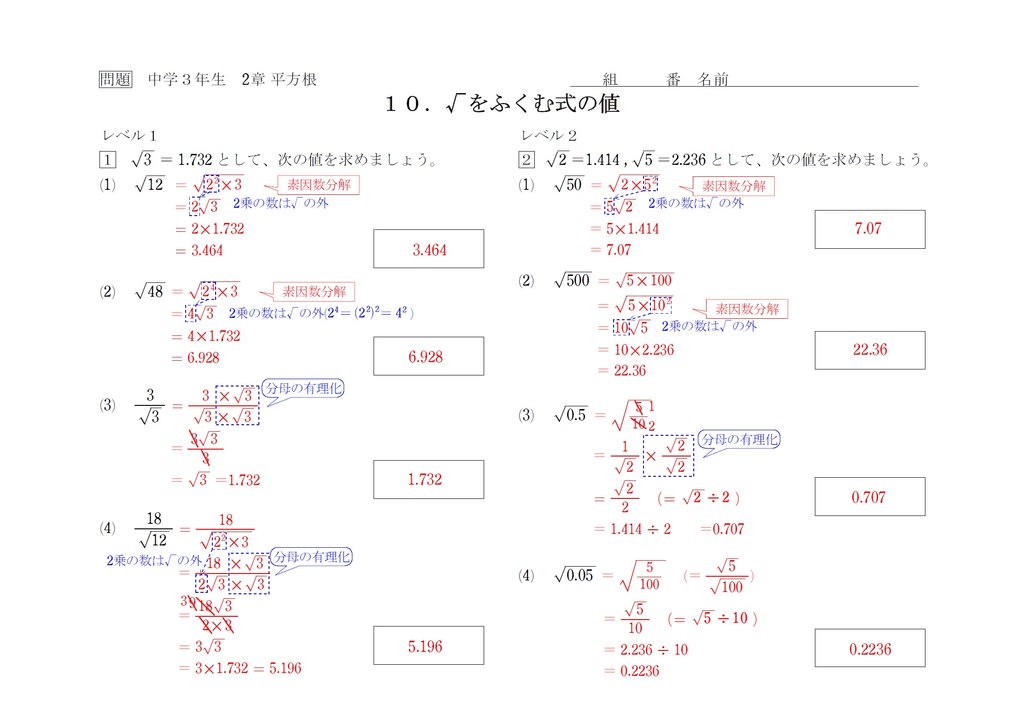
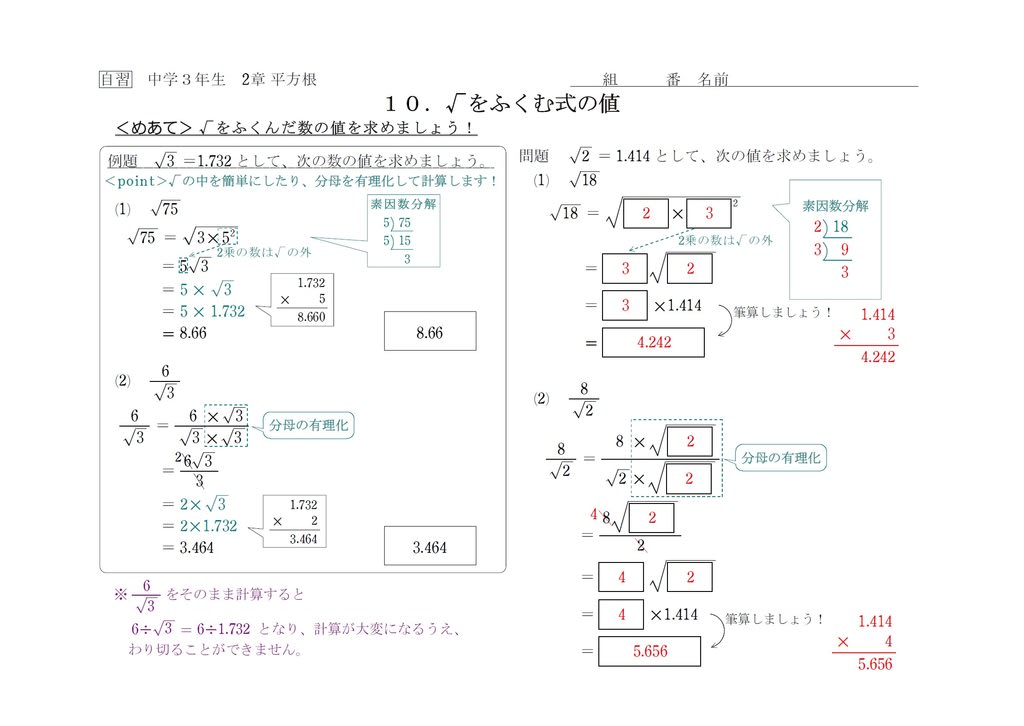
中3 平方根10 近似値 中学数学の勉強に
Jf (x) f (a)j < ε 任意のε について、あるδ を考えれば、a δ < x < aδ の範囲でf (a) とf (x) の差はε 以下である。 一様連続 8a 2 M (M に属する全ての点) について連続 中間値の定理 f (x) が区間a,b で連続でありf (aコラム テーラー展開(難易度1) 多くの関数f (x)は、abxcx 2 dx 3 ex 4 のような級数の形に展開することができます。 (この級数が収束する範囲内で) 例えば三角関数 sin x は のような無限級数となり、これはsin xのテーラー展開と呼ばれます。 関数f (x
ルート 展開 近似
ルート 展開 近似-1 1次近似—1次函数による近似 11 最初の例 111 例 f(x)=x2 (1) について考えよう。x を x =1(x1) (2) のように1とx1 の和に分けて、(1)に代入して展開すると、 f(x)=x 2= {1(x1)} = 12(x1)(x1)2 (3) となる。 今、x の値が非常に1に近い時、言い換えるとx1 の絶対値が非常に小さいときを考え こんにちは!ほけきよです。 皆さん、πを知っていますか??あの314以降無限に続く円周率です。 昔、どこかのお偉いさんが「314って中途半端じゃね?www3にしようぜ」 とかいって一時期円周率が3になりかけました。でもそれは円じゃなくて六角形だからだめです。
1次の近似値を用いて次の数の近似値を求めよ ただしp 3 14ル Yahoo 知恵袋
テイラー展開(テーラー展開, Taylor expansion)・マクローリン展開 (Maclaurin expansion) は,関数のべき級数展開と言えます。まずはその定義と感覚的な理解,そして具体例を述べ,そして無限回微分可能であっても,マクローリン展開できないような関数も触れましょう。 質問日時: 1548 回答数: 2 件 1>>rの時、近似式(1+r)^n≒1+nrは有名な式ですが、 私はこの式は2項定理から証明するものだと思っていたので、 nが自然数限定だと思っていたのですが、 今日、参考書でn=-1の時にこの近似式を使っているもの ルート・平方根の計算方法・仕方の3つのコツ ルート計算のコツはつぎの3つだ。 ルートを簡単にする 足し算・引き算はべつもの 分母は有理化しとく 練習問題をといてみよう。 つぎのルートの計算をしてください。 √8 √2分の5 – √3 × √5 コツ1
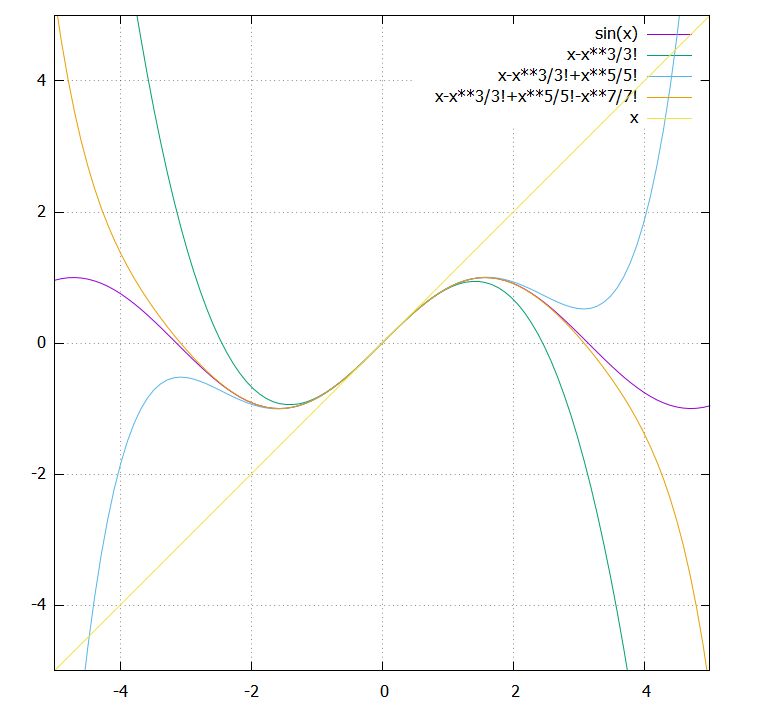
追記 @scivola さんのコメントより一部修正させて頂きました。修正箇所は下段コメントをご確認ください。 テイラー展開の応用 テイラー級数を応用し、平方根などの近似を求めよう 1 x のk乗のテイラー級数への展開になる。1次の近似分数は1=4 で、1年に本当の日数は1=4 日多いというわけで、4年に1 度閏年を設けて、1日増やしておかないといけないことになる。 しかし、2次の近似分数は 1 41 7 = 7 29 日となり、100年の間に100× 7 = テイラー展開とは、関数 f ( x) を多項式で近似する手法です。 という条件下において、 f ( x) は以下のような無限級数で表すことができます。 この式のことを、 「 f ( x) の a を中心としたテイラー展開」 と言います。 テイラー展開は、 a = 0 の場合につい
ルート 展開 近似のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 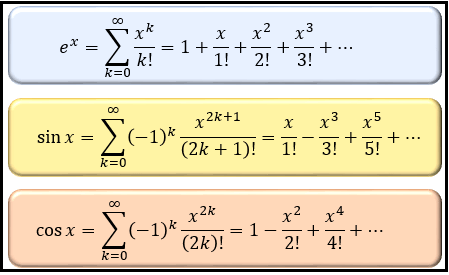 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
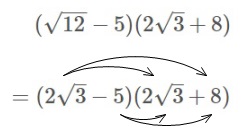 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 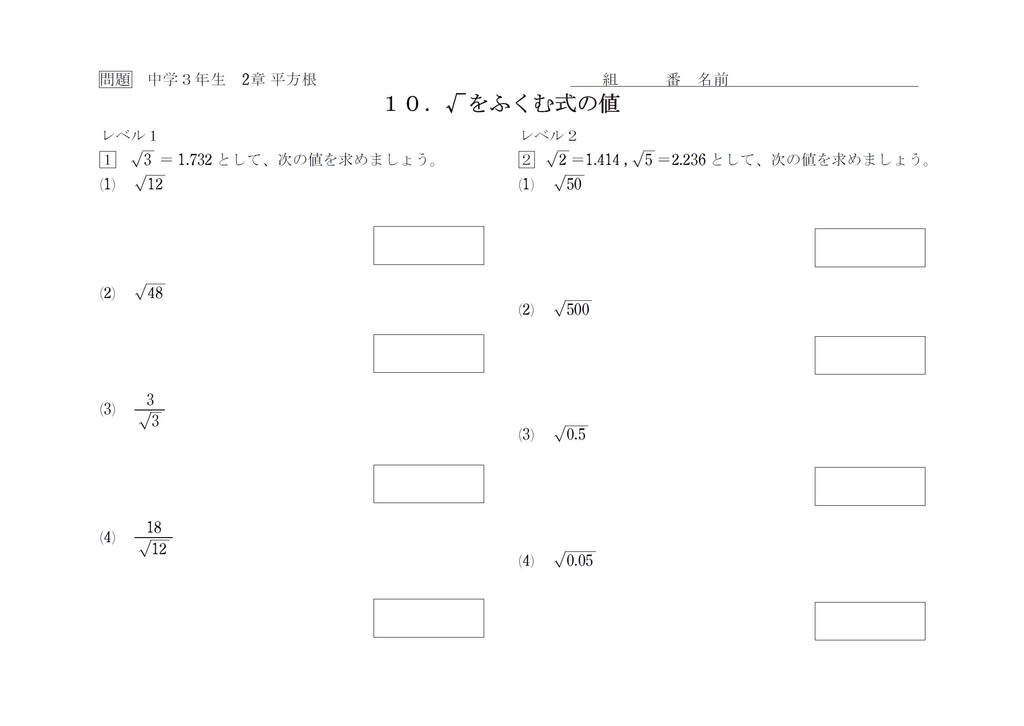 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 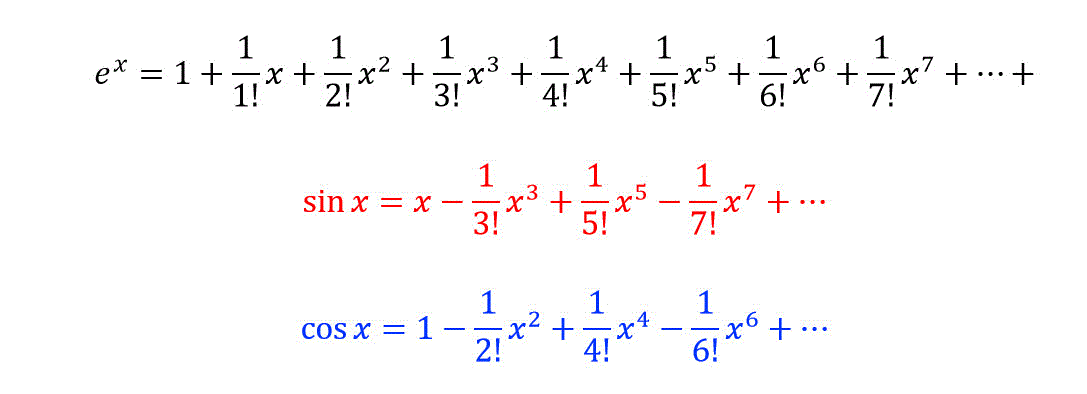 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
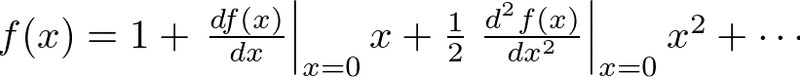 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
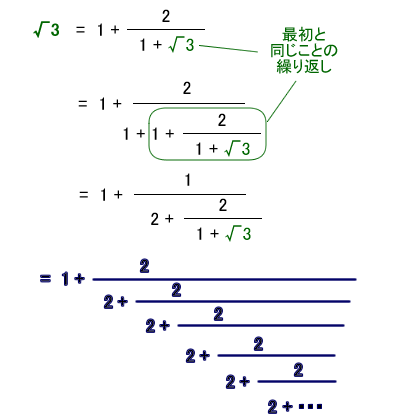
can******** さん 056 1 1 回答 √15の近似値を求めよという問題がわかりません お願いします √15の近似値を求めよという問題がわかりません お願いします √15=4√{1 (1/16)}を利用してxの2乗までマクローリン展開を求めて計算せよと書いてあり近似分数 連分数展開を適当な有限項で打ち切ると近似分数が得られます。 これは「本当は有理数なのだけど分母が分からない」という近似値が与えられたときに、 分母を推定するための強力な武器とな
Incoming Term: ルート 展開 近似,
コメント
コメントを投稿